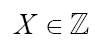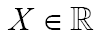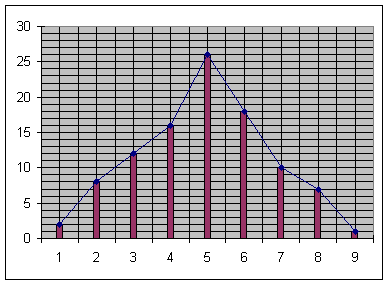
تتميز الكائنات الحية بمجموعة  من الصفات الكمية التي يمكن  قياسها و دراستها إحصائيا و تنعث بالمتغيرات ، نذكر من بينها الوزن،الطول،عدد البذور في الثمرة،عدد المواليد بالنسبة لكل حمل،كمية الحليب المنتجة من طرف الأبقار،نسبة الكولسترول في الدم ، قيمة الضغط الشرياني عند الإنسان...

 و تكون المتغيرات متواصلة عندما تأخذ قيمة المتغير كل مجالات التغير في حين  تنعث  بغير المتواصلة حين لا تأخذ قيم المتغير كل مجالات التغير.

 I ـ دراسة التغير غير المتواصل :

  تمت دراسة عدد المواليد بعد كل حمل عند ساكنة مكونة من 100 فأرة فتم الحصول على النتائج التالية:

المتغير  في هذا المثال يأخذ فقط الأرقام الصحيحة دون العشرية فهو غير متواصل.(لا تأخذ قيم المتغير كل مجالات التغير)

تبدأ الدراسة بالتمثيل البياني لتوزيع المتغير بدلالة التردد ، فنحصل على أخطوط عصوي(انظر الوثيقة) و نربط النقط المشكلة لكل قمة  بواسطة خطوط مستقيمة فنحصل على مضلع الترددات.

     بتسوية حدود مضلع الترددات نحصل على منحنى الترددات.

     – تطبيق

 يمثل الجدول الثاني توزيع تردد عدد البذور داخل سنفات gousse الفاصوليا:

1- حدد معللا جوابك طبيعة التغير المدروس.

2- أنجز التمثيل البياني لهذا المتغير.

II ـ دراسة التغير المتواصل:

  تمت دراسة كمية الحليب المنتجة في اليوم(Kg ) عند جماعة من الأبقار المستوردة مكونة من 50 فرد، فتم الحصول على النتائج التالية:

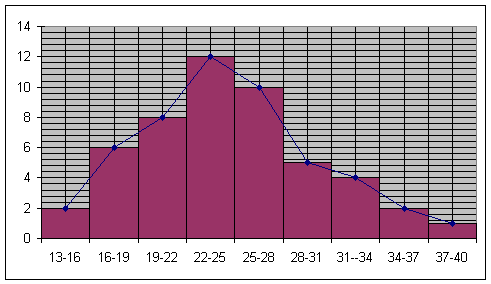
المتغير في هذا المثال يأخذ قيم متراوحة بين 13 و 40 حتى الأرقام العشرية لذلك ينعت المتغير  بكونه متواصلا .في هذه الحالة نقوم بتجميع القياسات داخل أقسام لها نفس وسع المجال(  3  في هذا المثال) و يصبح التوزيع إذن عبارة عن متتالية من الأقسام .

 نضع على محور الأفاصيل المتغير ( كمية الحليب) و على محور الأراتيب التردد المناسب (عدد الأبقار) ثم ننجز التمثيل البياني.نحصل على مدراج الترددات و بربط النقط المشكلة لمركز كل قسم بواسطة خطوط مستقيمة نحصل على مضلع الترددات.

 بتسوية حدود مضلع الترددات نحصل على منحنى الترددات.

        تطبيق :

 قمنا بوزن كتلة البذور عند جماعة من الفاصوليا،ويظهر الجدول التالي توزيع تردد هذه البذور حسب الوزن:

1- حدد معللا جوابك طبيعة التغير المدروس.

2- أنجز التمثيل البياني لهذا المتغير.

    يبقى التمثيل البياني غير كافي لإعطاء  فكرة واضحة عن مدى تغير الساكنة و إبراز خاصيات هذا التغير، لدا يتم اللجوء إلى بعض الخاصيات الإحصائية يطلق عليها ثابتات توزيع الترددات.

III ـ ثابتات توزيع ترددات تغير الصفات الوراثية الكمية داخل الجماعة:

1 - ثابتات الموضع:

      ـ المنوال: يقابله قيمة المتغير الأكثر ترددا بالنسبة للتغير غير المتواصل و  قيمة وسط القسم الأكثر ترددا بالنسبة للتغير المتواصل 

      ـ المعدل الحسابي: نستعمل المعادلة التالية

 بحيث:  xi تمثل قيمة المتغير و ni عدد الأفراد المقابل للمتغير (قد يرمز إليه اصطلاحا fi ) و N مجموع عدد الإفراد و Σ المجموع.

قد يكون لعينتين من نفس النوع، نفس المعدل الحسابي لكن ليس لهما نفس التبدد حول هذا المعدل(انظر المبيان التالي)،لهذا يتم اللجوء إلى استعمال ثابتات التبدد.

  تطبيق :

  يظهر الجدول التالي توزيع تردد الثمار عند جماعة من الطماطم حسب الكتلة:

1- حدد معللا جوابك منوال التغير المدروس.

2- أحسب المعدل الحسابي.

2- ثابتات التبدد :

        ـ الفارق الوسطي الحسابي:  يتم حسابه باستعمال المعادلة التالية:

    رغم أهمية الفارق الوسطي الحسابي  إلا أنه غالبا ما يكون غير كافي لتحديد مدى تبدد القياسات المحصل عليها

       لهذا نلجأ إلى تحديد معيارين آخرين هما المغايرة والانحراف النمطي.

         ـ  المغايرة:و تحدد بالعلاقة التالية:

         ـ الانحراف النمطي المعياري:و هو الجذر التربيعي للمغايرة

σ=√V

 يستعمل الانحراف النمطي و المعدل الحسابي لحساب مجال الثقة الذي يأخذ الدلالات التالية:

منحنى Gauss

         ـ معامل التغير:  يتم حسابه باستعمال المعادلة التالية:

تطبيق :

  يظهر الجدول التالي نتائج القياس الإحيائي لطول سويقات أزهار جماعة نباتية

1- حدد معللا جوابك طبيعة التغير المدروس.

2- أنجز التمثيل البياني لهذا المتغير.

3- أحسب ثابتات الموضع و ثابتات التبدد .

4 ـ ماذا تستنتج؟

IV ـ  الاصطفاء داخل جماعة : تحديد مفهوم السلالة النقية:

  يمثل المبيان التالي نتائج القياس الإحيائي لوزن البذور عند جماعة من الفاصوليا:

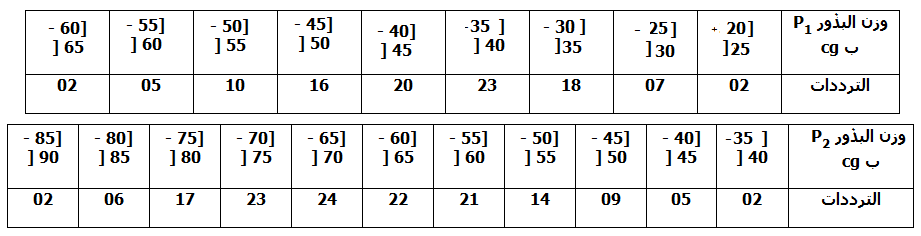
   يتبين أن المنحنى المحصل عليه أحادي المنوال مما قد يوحي إلى تجانس هذه الجماعة بالنسبة لصفة الوزن.

نقوم بانتقاء عينتين من بذور هذه الجماعة: العينة الأولى خفيفة الوزن بين 20cg و 25cg  و العينة الثانية ثقيلة الوزن بين 85cg و 90cg

و نقوم بزرع العينتين في وسطين معزولين عن بعضهما البعض،بحيث تخضع كل عينة بعد الإنبات و الازهرار، للإخصاب الذاتي

 بعد الإثمار أعطت الدراسة الإحصائية للبذور المحصل عليها،النتائج التالية:

 بانجازنا للتمثيل البياني نحصل على النتائج التالية:

 نلاحظ أنه تم الحصول على مضلعين للتردد أحاديي المنوال ، متفاوتي المنوال فيما بينهما و مع منوال الجماعة P .

 إذن فالجماعة P  غير متجانسة بالنسبة للصفة المدروسة، و قد حصلنا بعد الانتقاء على جماعتين مختلفتين P1 و P2  كلاهما تشكل سلالة.و يكون الانتفاء قي هذه الحالة فعالا لأنه انطلاقا من السلالة P أمكننا الحصول على سلالتين مختلفتين P1 و P2 .

للكشف عن تجانس السلالتينP1 و P2 نكرر نفس التجربة بالنسبة لكل سلالة و نلاحظ النتائج ، فإذا حصلنا على نفس المنوال بالنسبة لكل سلالة فسيكون الانتقاء غير فعال(لم تتغير النتائج) و نعتبر السلالات نقية في هذه الحالة.

www.khayma.com/fatsvt